Lambert maneuvers and trails in plots

What's new?

Three weeks have passed since the coding phase began and new features have been added to the software:

• Lambert is now a Maneuver instance.
• A trail keyword in StaticOrbitPlotter for showing orbits' trails.

Lambert just needs now two orbits!

Although the raw algorithms are kept under the module poliastro.iod, it is possible now to simplify the process of solving this famous astrodynamics problem by making use of the poliastro.maneuver module.

Imagine that we want to solve the classical problem ongoing from Earth to Mars for a trip of 600 days duration. Let us compare before and after Maneuver.lambert implementations:

With 0.12 version:

from astropy import units as u
from astropy.time import Time

from poliastro.bodies import Earth, Mars, Sun
from poliastro.iod.izzo import lambert
from poliastro.twobody import Orbit

LAUNCH = Time.now()
ARRIVAL = LAUNCH + 600 * u.day
TOF = ARRIVAL - LAUNCH

ss_earth = Orbit.from_body_ephem(Earth, epoch=LAUNCH)
ss_mars = Orbit.from_body_ephem(Mars, epoch=ARRIVAL)

(dv_a, dv_b), = lambert(Sun.k, ss_earth.r, ss_mars.r, tof=TOF)
ss_trans = Orbit.from_vectors(Sun, ss_earth.r, dv_a)
ss_target = Orbit.from_vectors(Sun, ss_mars.r, dv_b)

Notice that we work with a raw Lambert's algorithm. Therefore, we needed to pass the gravitational parameter, initial position, final one and finally the time of flight. After that the transfer and target orbits are created.

However with the 0.13 version this process will be not only simplified but more intuitive:

from astropy import units as u
from astropy.time import Time

from poliastro.bodies import Earth, Mars
from poliastro.maneuver import Maneuver
from poliastro.twobody import Orbit

LAUNCH = Time.now()
ARRIVAL = LAUNCH + 600 * u.day

ss_earth = Orbit.from_body_ephem(Earth, epoch=LAUNCH)
ss_mars = Orbit.from_body_ephem(Mars, epoch=ARRIVAL)

man_lambert = Maneuver.lambert(ss_earth, ss_mars)
ss_trans, ss_target = ss_earth.apply_maneuver(man_lambert, intermediate=True)

Although we have the same number of imports, the fact that we have a Maneuver instance, as a result, is very powerful. It not only contains all the different impulses but also can be applied to the departure orbit. This means that we do not care anymore about working with vectors and times but with Orbit instances, which are the core of poliastro.

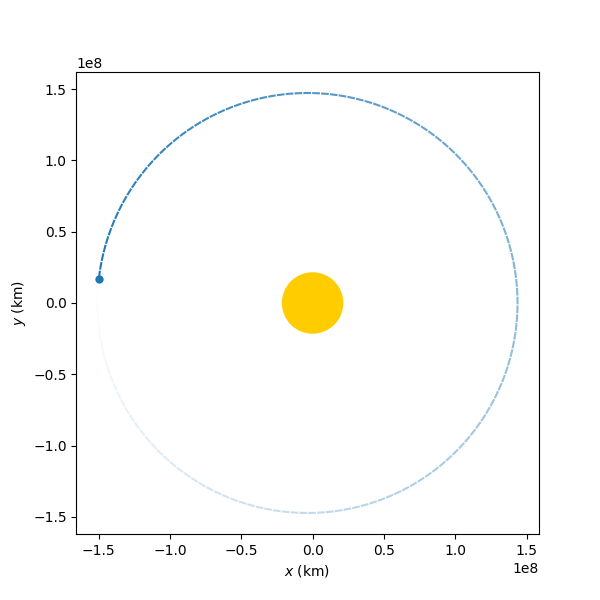
Trails can now be plotted

When it comes to plotting, it is very difficult to recreate movement on static images. And if we also add the fact that representing a 3D trajectory on a two-dimensions plot sometimes can lead to confusion, things get even worst.

For that, and with a lot of Juanlu's help, we finally implemented a trail option that fades any orbit trajectory, giving the user the feeling that that object was moving along the drawn path when the plot was made. It works with the StaticOrbitPlotter class just by passing the argument trail=True:

import matplotlib.pyplot as plt
poliastro.bodies import Earth
froms.plotting.static import StaticOrbitPlotter
from poliastro.twobody import Orbit                                             

ss_earth = Orbit.from_body_ephem(Earth)
plotter = StaticOrbitPlotter()
plotter.plot(ss_earth, trail=True)
plt.show()

Astropy 3.2

Astropy 3.2 was tagged and some poliastro tests were failing. Most of the are related with astroquery, since the JPL database was updated.

In particular, some tiny precission errors appeared but they were solved easily after deleting the astropy's caché file. However, something that needs a further inspection is the last failing test related to the new GeocentricSolarEcliptic. A deep inspection on Astropy's changelog is needed on solving this.

For the next weeks

For the next weeks, I am planning to solve the previous issue and updating the user's guide to the new Lambert maneuver. Also, since working on this topic, a multi-revolution example will be added to the documentation and minor errors in Lambert's algorithms need further inspection.

However, Gauss' algorithm is still something that frustrates me. It is supposed that it will properly propagate any orbit no matter it's nature and therefore may be the solution to near-parabolic orbits. But for the moment, I have not succeeded in implementing this algorithm. I hope it to be ready for the end of this month!